接續昨天的初版特徵,用隨機森林的模型訓練後於Kaggle上的分數為73.54%準確率。雖然不差,但還有許多改善空間。分數不佳的原因在於前一篇文章中採用的處理缺漏值的策略太過陽春,本篇將以兩點改進方向做分享,演示從73.54%的準確率改善到79.84%的過程:
[Titanic船艙示意圖]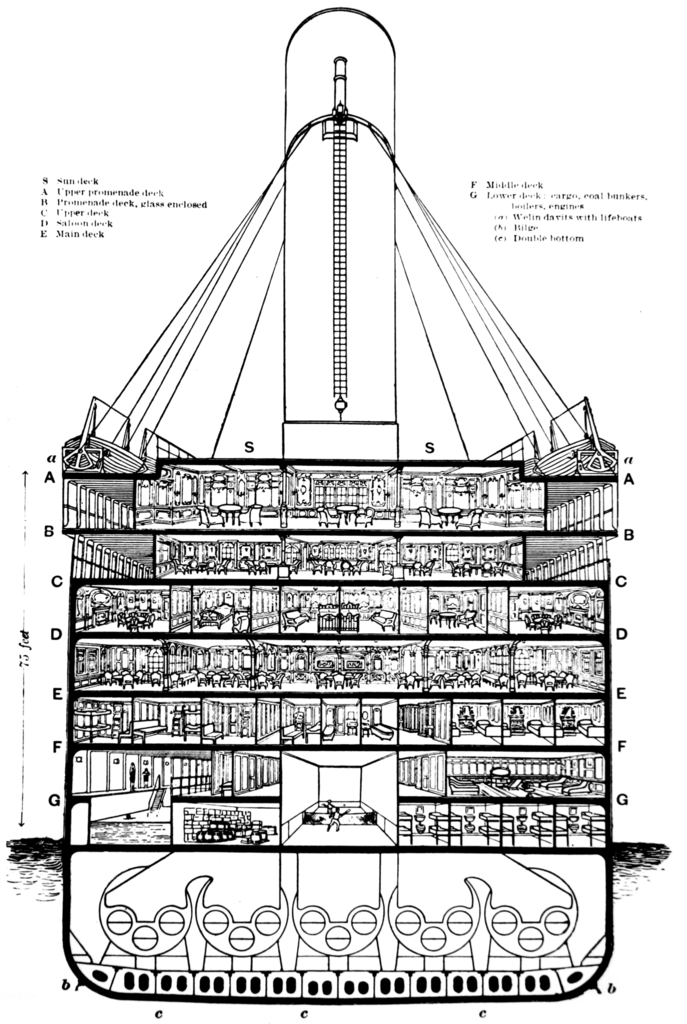
Cabin資料無缺漏的乘客紀錄的存歿數目EDA(0為已歿,1為生還):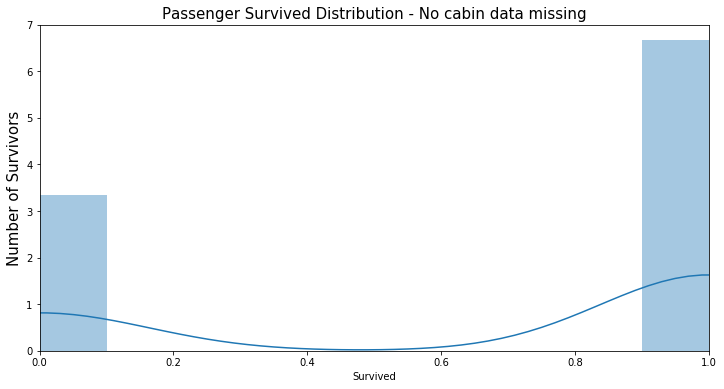
Cabin資料缺漏的乘客紀錄的存歿數目EDA(0為已歿,1為生還):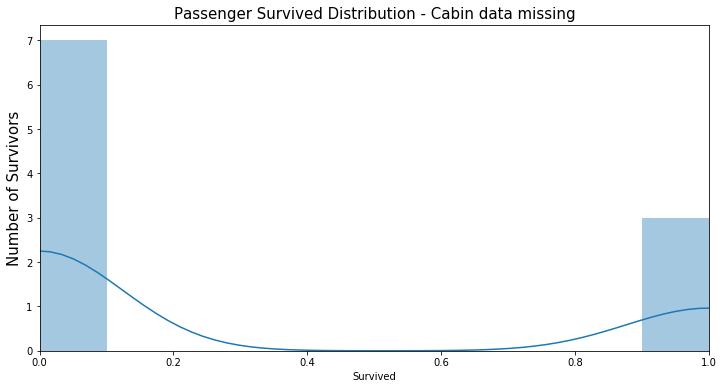
透過EDA可以看到一開始看似缺漏嚴重而被我們棄用的此欄位其實有隱含的訊息。資料有缺漏的乘客的死亡人數占所有資料缺漏人數的7成左右,而Cabin資料無缺漏的乘客死亡人數也正好是3成左右。這個現象正好是一個有用的特徵,換句話說,在此批資料中,如果我們以Cabin欄位是否有紀錄來猜測乘客的生存與否,會有70%左右的準確率,明顯比隨機猜測的結果還好多了。
再進一步做更多的EDA,發現資料無缺漏的族群幾乎都是客戶等級最高的人,反之資料缺漏的族群大部分是客戶等級最低的: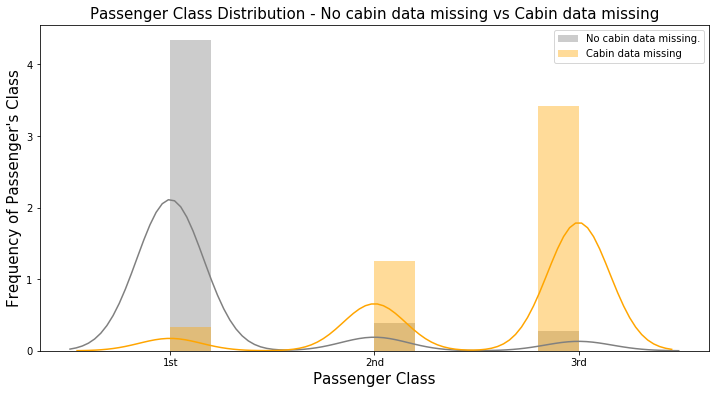
甚至年齡分布在此兩者間都有明顯差異: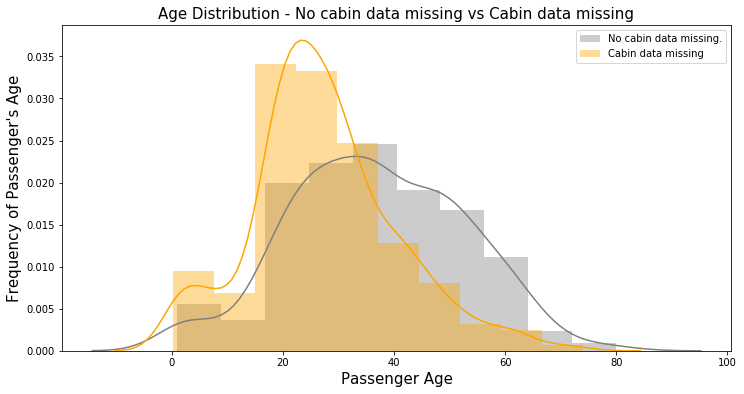
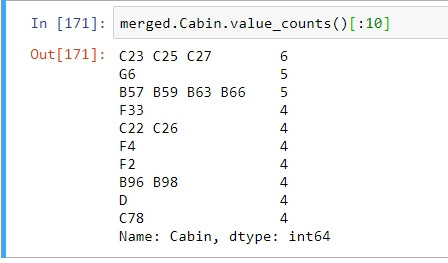
經過EDA後證實Cabin其實是一有用的欄位,因此下一步作為應是解析此欄位。如下圖,Carbin欄位中包含的資料可能代表了乘客所訂鐵達尼上的房間編號,並以英文字母作為房間在船上的特定區塊的代號,數字則表示房號。也因此我們能夠從中獲得相當多的訊息;乘客訂了多少的房間、房號的差距可代表房間距離、乘客的家人平均多少人住在一個房間內、乘客訂了複數的房間是否有跨區...等等,諸多的可能隱含與生存率有關連的訊息。
填補缺漏值一般的方式如前一篇文章提到,使用0,-999,mean,median等等來填補以外,也有更聰明的方式。
分類與迴歸為機器學習重要也最普遍的兩個任務,因此可以幫助我們預測乘客的生存與否(分類),也能夠幫助我們預測乘客年齡,僅僅是輸入特徵些微的不同以及輸出的差異。那麼機器學習將如何幫助我們在填補缺漏值呢?一個實例是使用線性迴歸模型:我們以titanic資料集內除了Sruvived/Age以外的其他所有表徵作為模型訓練的輸入,而Age是我們欲預測的目標。因此,透過輸入給此模型一筆客戶的特定表徵就能幫助我們預估該客戶的年齡,也就能夠一一幫我們估計年齡缺漏的客戶的年齡。
善用資料中的訊息來做分析,例如:Name欄位中含有乘客的稱謂,稱謂間接或直接反映了年齡因素,例如Mrs.與Miss的差別在於已婚與否,自然在年齡上會有所區別,比起沒有根據的決定填補值更有用。
例:圖為稱謂為Master的乘客年齡分布圖,算術平均數為5.5左右,而前一篇的填值策略為使用全部乘客年齡的算術平均數作為填補資料,數值為30左右,與真實數值相去甚遠以外也可說是降低了資料品質。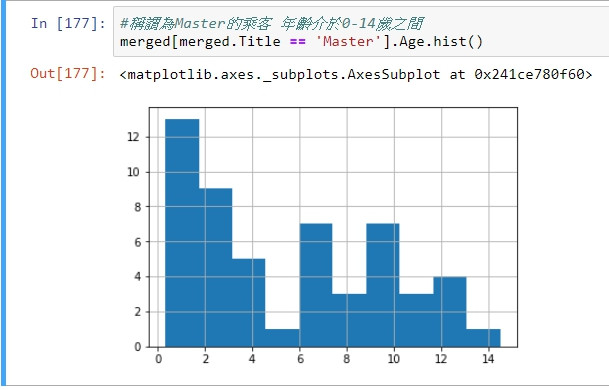
以其他與本紀錄特徵值相近的紀錄來做補值也是一種常見做法,例如:以10歲的年輕孩童族群為例,這些年輕孩童不大可能會有子嗣,因此特徵會較相近,Parch(在鐵達尼上的父母或子嗣的數目)不超過2、SibSp(在鐵達尼上的兄弟姊妹的數目)可能會較多,反之已婚的中年男女在Parch欄位中的數量會相較多一點而SibSp少,因此以特徵值相近的紀錄做填補依據也是一個不錯的作法。
圖為特徵相近的乘客紀錄:有五個特徵(稱謂、在船上的親人數目、乘客等級、性別)相同的三個人年齡相當的接近。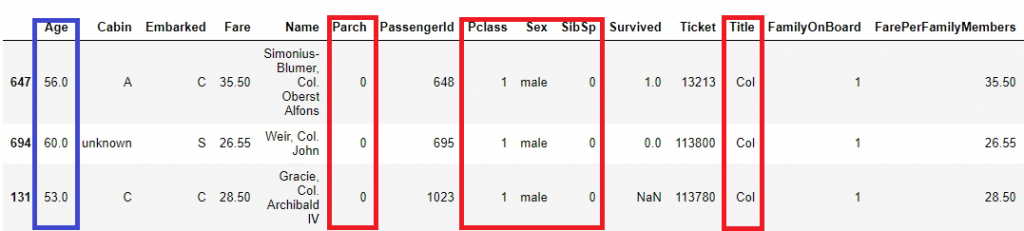
透過以下兩步驟的作法,我上繳Kaggle預測準確率從73%變為79.84%,相當大的跳動。
before: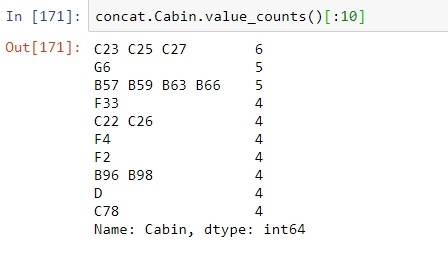
after: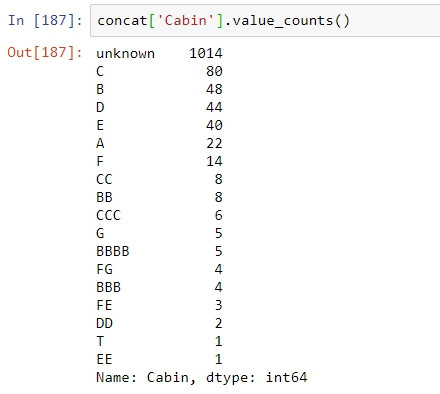
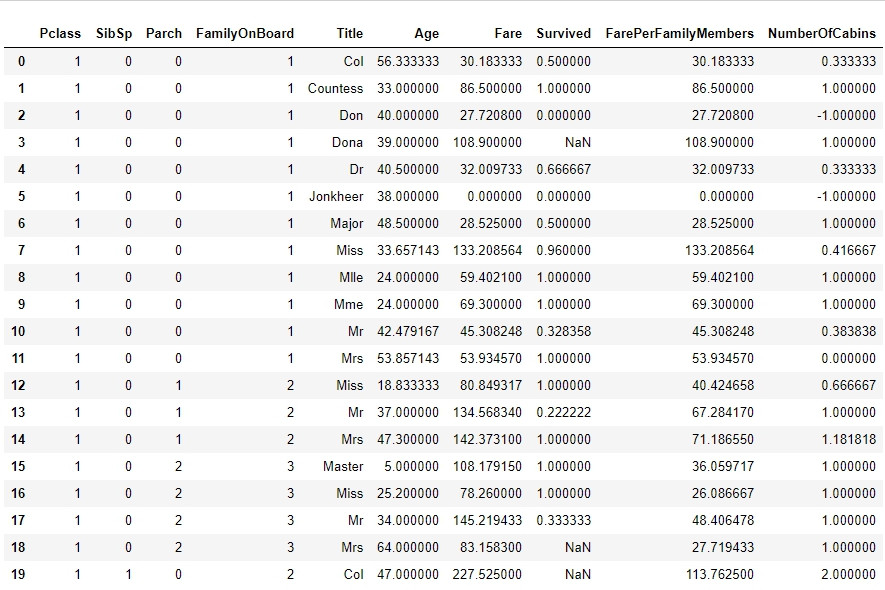
以此方法實測在年齡無缺值的紀錄上,以推估的年齡以及真實年齡做比較,推估的誤差平均在6左右,表現相當不錯。在文中提到的以機器學習做年齡預測用在填補缺漏值上表現則略遜一籌,rmse大約為10左右。
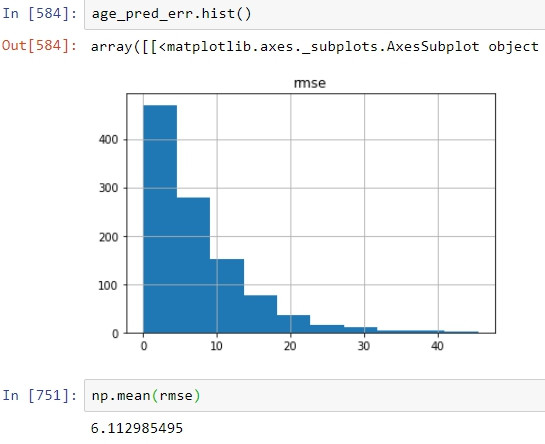
僅僅是兩個步驟,準確率就提升了一個檔次,但Cabin欄位的可利用程度還大有可為,如同文前有提到的,Cabin欄位可以衍生出訂房數量進而再出現更多有意思的參數,我將繼續努力探索並分享未來的發現以及解決方案。
